gftool.fourier.tau2izp

gftool.fourier.tau2izp(gf_tau, beta, izp, moments=None, occ=False, weight=None)

Fourier transform of the real Green’s function gf_tau to izp.

Fourier transformation of a fermionic imaginary-time Green’s function to fermionic imaginary Padé frequencies izp. We assume a real Green’s function gf_tau, which is the case for commutator Green’s functions \(G_{AB}(τ) = ⟨A(τ)B⟩\) with \(A = B^†\). The Fourier transform gf_iw is then Hermitian. If no explicit moments are given, this function removes \(-G_{AB}(β) - G_{AB}(0) = ⟨[A,B]⟩\).

TODO: this function is not vectorized yet.

Parameters

gf_tau(N_tau) float np.ndarray

The Green’s function at imaginary times \(τ \in [0, β]\).

betafloat

The inverse temperature \(beta = 1/k_B T\).

izp(N_izp) complex np.ndarray

Complex Padé frequencies at which the Fourier transform is evaluated.

moments(m) float array_like, optional

High-frequency moments of gf_iw. If none are given, the first moment is chosen to remove the discontinuity at \(τ=0^{±}\).

occfloat, optional

If given, fix occupation of Green’s function to occ. (default: False)

weight(…, N_tau) float np.ndarray, optional

Weight the values of gf_tau, can be provided to include uncertainty.

Returns

gf_izp(N_izp) complex np.ndarray

The Fourier transform of gf_tau for given Padé frequencies izp.

See also

tau2iw

Fourier transform to fermionic Matsubara frequencies.

pole_gf_from_tau

Function handling the fitting of gf_tau

Notes

The algorithm performs in fact an analytic continuation instead of a Fourier integral. It is however only evaluated on the imaginary axis, so far the algorithm was observed to be stable

Examples

>>> BETA = 50
>>> tau = np.linspace(0, BETA, num=2049, endpoint=True)
>>> izp, __ = gt.pade_frequencies(50, beta=BETA)

>>> poles = 2*np.random.random(10) - 1  # partially filled
>>> weights = np.random.random(10)
>>> weights = weights/np.sum(weights)
>>> gf_tau = gt.pole_gf_tau(tau, poles=poles, weights=weights, beta=BETA)
>>> gf_ft = gt.fourier.tau2izp(gf_tau, beta=BETA, izp=izp)
>>> gf_izp = gt.pole_gf_z(izp, poles=poles, weights=weights)

>>> import matplotlib.pyplot as plt
>>> __ = plt.plot(gf_izp.imag, label='exact Im')
>>> __ = plt.plot(gf_ft.imag, '--', label='FT Im')
>>> __ = plt.plot(gf_izp.real, label='exact Re')
>>> __ = plt.plot(gf_ft.real, '--', label='FT Re')
>>> __ = plt.legend()
>>> plt.show()

(png, pdf)

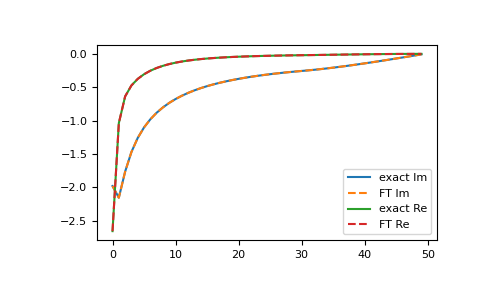
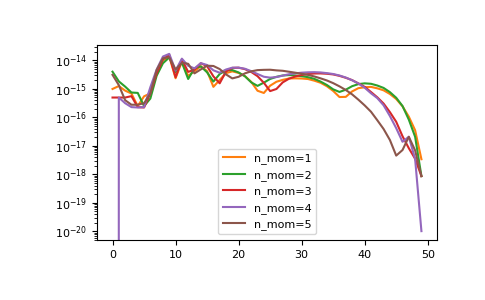
Results of tau2izp can be improved giving high-frequency moments.

>>> mom = np.sum(weights[:, np.newaxis] * poles[:, np.newaxis]**range(6), axis=0)
>>> for n in range(1, 6):
...     gf = gt.fourier.tau2izp(gf_tau, izp=izp, moments=mom[:n], beta=BETA)
...     __ = plt.plot(abs(gf_izp - gf), label=f'n_mom={n}', color=f'C{n}')
>>> __ = plt.legend()
>>> plt.yscale('log')
>>> plt.show()

(png, pdf)

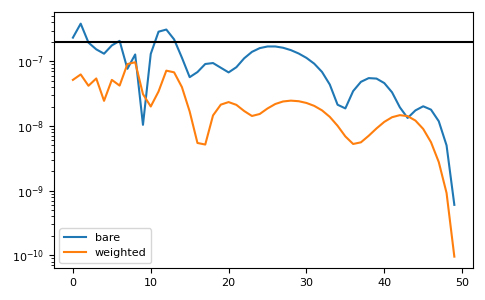
The method is resistant against noise, especially if there is knowledge of the noise:

>>> magnitude = 2e-7
>>> noise = np.random.normal(scale=magnitude, size=gf_tau.size)
>>> gf = gt.fourier.tau2izp(gf_tau + noise, izp=izp, moments=(1,), beta=BETA)
>>> __ = plt.plot(abs(gf_izp - gf), label='bare')
>>> gf = gt.fourier.tau2izp(gf_tau + noise, izp=izp, moments=(1,), beta=BETA,
...                         weight=abs(noise)**-0.5)
>>> __ = plt.plot(abs(gf_izp - gf), label='weighted')
>>> __ = plt.axhline(magnitude, color='black')
>>> __ = plt.legend()
>>> plt.yscale('log')
>>> plt.tight_layout()
>>> plt.show()

(png, pdf)

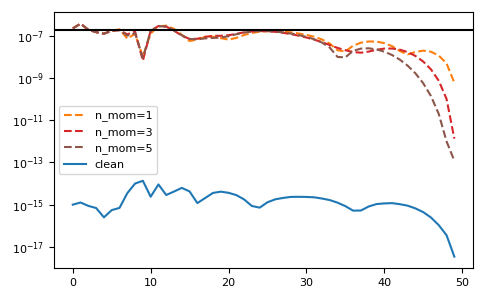
>>> for n in range(1, 7, 2):
...     gf = gt.fourier.tau2izp(gf_tau + noise, izp=izp, moments=mom[:n], beta=BETA)
...     __ = plt.plot(abs(gf_izp - gf), '--', label=f'n_mom={n}', color=f'C{n}')
>>> __ = plt.axhline(magnitude, color='black')
>>> __ = plt.plot(abs(gf_izp - gf_ft), label='clean')
>>> __ = plt.legend()
>>> plt.yscale('log')
>>> plt.tight_layout()
>>> plt.show()

(png, pdf)