gftool.fourier.iw2tau_dft

gftool.fourier.iw2tau_dft(gf_iw, beta)

Discrete Fourier transform of the Hermitian Green’s function gf_iw.

Fourier transformation of a fermionic Matsubara Green’s function to imaginary-time domain. The infinite Fourier sum is truncated. We assume a Hermitian Green’s function gf_iw, i.e. \(G(-iω_n) = G^*(iω_n)\), which is the case for commutator Green’s functions \(G_{AB}(τ) = ⟨A(τ)B⟩\) with \(A = B^†\). The Fourier transform gf_tau is then real.

Parameters

gf_iw(…, N_iw) complex np.ndarray

The Green’s function at positive fermionic Matsubara frequencies \(iω_n\).

betafloat

The inverse temperature \(beta = 1/k_B T\).

Returns

gf_tau(…, 2*N_iw + 1) float np.ndarray

The Fourier transform of gf_iw for imaginary times \(τ \in [0, β]\).

See also

iw2tau_dft_soft

Fourier transform with artificial softening of oszillations

Notes

For accurate an accurate Fourier transform, it is necessary, that gf_iw has already reached it’s high-frequency behaviour, which need to be included explicitly. Therefore, the accuracy of the FT depends implicitely on the bandwidth!

Examples

>>> BETA = 50
>>> iws = gt.matsubara_frequencies(range(1024), beta=BETA)
>>> tau = np.linspace(0, BETA, num=2*iws.size + 1, endpoint=True)

>>> poles = 2*np.random.random(10) - 1  # partially filled
>>> weights = np.random.random(10)
>>> weights = weights/np.sum(weights)
>>> gf_iw = gt.pole_gf_z(iws, poles=poles, weights=weights)
>>> # 1/z tail has to be handled manually
>>> gf_dft = gt.fourier.iw2tau_dft(gf_iw - 1/iws, beta=BETA) - .5
>>> gf_iw.size, gf_dft.size
(1024, 2049)
>>> gf_tau = gt.pole_gf_tau(tau, poles=poles, weights=weights, beta=BETA)

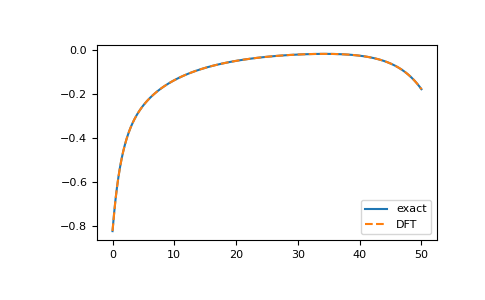
>>> import matplotlib.pyplot as plt
>>> __ = plt.plot(tau, gf_tau, label='exact')
>>> __ = plt.plot(tau, gf_dft, '--', label='DFT')
>>> __ = plt.legend()
>>> plt.show()

(png, pdf)

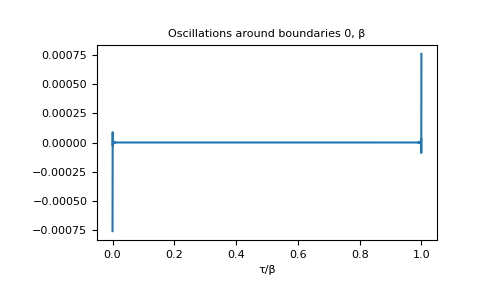
>>> __ = plt.title('Oscillations around boundaries 0, β')
>>> __ = plt.plot(tau/BETA, gf_tau - gf_dft)
>>> __ = plt.xlabel('τ/β')
>>> plt.show()

(png, pdf)

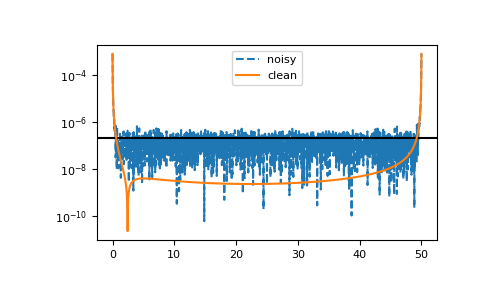
The method is resistant against noise:

>>> magnitude = 2e-7
>>> noise = np.random.normal(scale=magnitude, size=gf_iw.size)
>>> gf_dft_noisy = gt.fourier.iw2tau_dft(gf_iw + noise - 1/iws, beta=BETA) - .5
>>> __ = plt.plot(tau, abs(gf_tau - gf_dft_noisy), '--', label='noisy')
>>> __ = plt.axhline(magnitude, color='black')
>>> __ = plt.plot(tau, abs(gf_tau - gf_dft), label='clean')
>>> __ = plt.legend()
>>> plt.yscale('log')
>>> plt.show()

(png, pdf)